Scalazの型クラス

Validationの定義を調べるついでにScalazの型クラスの継承関係などを調べたのでまとめておきます。

Monad

Monad関係の型クラスの継承関係は以下のようになります。

整理すると、Monad、Applicative Functor、Pointed Functor、Functorはそれぞれ以下の性質を持っていることになります。

	Functor	Pure	Apply	Bind
Functor	◯	-	-	-
Pointed Functor	◯	◯	-	-
Applicative Functor	◯	◯	◯	-
Monad	◯	◯	◯	◯

Functor＆Pureは型クラスPointedとして定義されています。Pointed Functorと呼ぶこともあるようです。

Applicative Functorの型クラスApplicativeはFunctor＆Pure＆Applyとなります。Applicative Functorのapply演算は型クラスApplyが提供します。

Monadの型クラスMonadはFunctor＆Pure＆Apply＆Bindとなります。Monadのunit演算、bind演算はそれぞれ型クラスPureと型クラスBindが提供します。Monadのjoin演算は型クラスとしては定義されていませんが、型クラスBindのbind演算から逆算する関数が定義されています。

機能順で示すと:

• Monad ＞ Applicative Functor ＞ Pointed Functor ＞ Functor

ということになります。型クラスPointed Functorは定義はありますが、実際に直接使用している所はほとんどないので実際はあまり意識することはありません。

代数的構造

代数的構造に関する型クラスの継承関係は以下のようになります。

型クラスSemigroupは半群(semigroup)、型クラスZeroは単位元(identity element)を記述する型クラスです。

型クラスMonoidは、型クラスSemigroupと型クラスZeroを継承した型クラスで、モノイド(monoid)を記述する型クラスです。

本来であれば、逆元(inverse element)や群(group)があってもよさそうですが、これらは定義されていないようです。もちろん、環(ring)や体(field)の定義もありません。

今の所、プログラミング言語の基本機能として有効な代数的構造はモノイド(半群、単位元)までということだと思います。

Scalazを使っていると、モノイドという数学(代数的構造)上の抽象概念が、プログラミングにおいて非常に便利なことを実感します。具体的には、モノイドは畳込み系(fold系)の演算で頻出します。

関数型プログラミングの「コメ」

モナドは、Scala本体でもflatMapメソッドのハードコーディングという荒業で実現していますが、Applicative Functorやモノイドについては今の所Scalazを使わないと利用することができません。また、モナドやファンクタも型クラスMonadや型クラスFunctorを使うことで、静的型付けの枠組みを活かしながら安全で発展的な運用を行うことができます。

Functor, Applicative Functor, Monad, Monoidが関数型プログラミングの「コメ」とするなら、現時点のScalaプログラミングではScalazを使うのが唯一の解ということになります。

並列プログラミング

代数的構造は、普通の関数型プログラミングでも有効な概念ですが、並列プログラミングではさらにその重要性が増すと考えています。ボクがScalazを使って代数的構造ベースのプログラミングの経験値を上げておきたいと考えているのも並列プログラミングが大きな動機となっています。

代数的構造に登場する結合律(associative law)、可換律(commutative law)、分配律(distributive law)は専門用語としてみると難しく感じますが、小学生の算数にも出てくる概念で、概念そのものは誰でも知っていることです。

• Commutative, Associative and Distributive Laws

ただし、これらの概念を任意のデータ構造とそれに対する演算に適用しようとすると、とたんに難しくなります。少なくても今までは普通のオブジェクト指向言語では、スコープ外の概念でした。

これが、HaskellやScala+Scalazといった現代風の関数型プログラミングで、始めて普通のプログラマの道具として使用できるようになったと認識しています。

この結合律、可換律、分配律が並列プログラミングでは非常に重要な概念になってくると推測しています。結合律、可換律、分配律を満たすオブジェクト群に対する演算は、処理の実行順番に対する制約が低くなるので、処理の最適化を自動化できる可能性が高まります。

メニーコア時代に入ると、一般のアプリケーションもネイティブな並列アプリケーションになってくると予測されるので、そうなれば一般のアプリケーション・プログラマにとっても基本的な素養となるということです。

結合律

結合律は現段階でもモノイドを用いて利用可能です。

たとえば、fold系の畳込みの対象がモノイドである場合には、畳込みの演算の評価順番が左からや右からといった制約がなくなるので、並列実行して処理の終わったところから畳み込んでいくといった最適化が可能になります。

具体的には「A + B + C」を「(A + B) + C」と計算しても、「A + (B + C)」と計算してもよいということですね。

分散カウンタ的なアルゴリズムをより汎用的な形で実現することにも使えそうです。分散カウンタの場合は、整数値の加算がモノイドであることを利用しているわけですが、これを任意のデータ構造に応用できるようになります。

型クラスMonoidを用いることで、こういったメカニズムを静的型付けで利用できるようになります。

可換律

結合律は型クラスMonoid(Semigroup)の導入ですでに実用化されていますが、次の課題は可換律です。

可換律を満たした演算は、結合律よりもさらに大きな最適化が可能になります。

前述のfold系の畳込みの例で言うと、畳込み対象が可換モノイドの場合は、畳込みの演算の評価順番だけでなく、演算の実行順番も変えることができます。

具体的には「A + B + C」を「(A + B) + C」と計算しても、「(A + C) + B」と計算してもよいということですね。並列処理では、どの処理がどの順番で完了するか事前に決定できないので、式の形を変形して実行順番を変えてよいというのは、非常に大きなアドバンテージになります。

前述の分散カウンタの例でも、整数の加算は可換モノイドでもあるので、この性質も利用可能です。任意のデータ構造に適用する場合も、モノイドより可換モノイドの方がより最適化された処理を実行することが可能になります。

現時点でのScalazでは定義されていませんが、いずれCommutativeSemigroupやCommutativeMonoidといった型クラスが登場して、これらの型クラスを使用した並列処理の関数などが登場するようになるのではないかと思います。Scalazでは、parMapメソッドやparBindメソッドでPromiseモナドを使った並列処理のファンクタ演算やモナド演算が使えますが、ここにCommutativeMonoidを対象としたparFoldReduceメソッドが提供されるというようなイメージです。

分配律

分配律は、二項演算が2つ登場してきて、難易度がぐっと上がってきます。代数的構造では環や体で分配律を扱いますが、プログラミングへの応用は当分先の話になりそうです。

Comonad

Monadの逆の動きをする型クラスComonad関連の型クラスです。

中心となるのが型クラスCojoinです。Scalazの型クラスには直接現れてきませんが、bind演算はmap演算+join演算です。このjoin演算がモナド演算の核となります。join演算は、入れ子になったモナドを一つにまとめる操作を行いますが、この操作時にそれぞれのモナド特有の結合処理を行うのが、モナド演算のミソとなっています。型クラスCojoinはこのjoin演算の逆演算をする型クラスです。つまり、単層のモナドから、モナドの入れ子を再構築します。

型クラスComonadは、このCojoinを利用して単層のモナドからモナドの入れ子を再構築します。

同様に型クラスCopureは型クラスPureの逆演算をする型クラスです。

Comonadは理屈は朧気(おぼろげ)ながらわかるのですが、実際のプログラミングでどのようなユースケースがあるのかは今の所判然としません。

ここでは存在を記録しておくにとどめておきます。

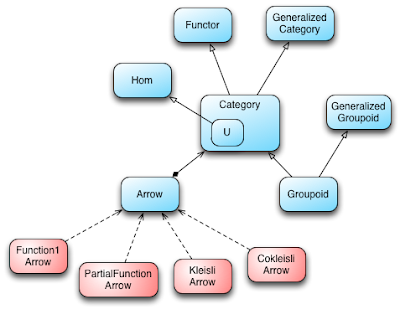
Category

ScalaやScalazのモナドは圏論の理論をプログラミングに応用した物です。その大元となる圏論の圏も型クラスCategoryとして型クラス化されています。

圏はオブジェクトと射(arrow、morphism)から構成されますが、この射を記述する型クラスがArrowです。

Category関連の型クラス群は、型クラスArrowの型クラスインスタンスが分からないと、プログラミングとの接点が見えてこないので、図に入れています。

• Function1Arrow
• PartialFunctionArrow
• KleisliArrow
• CokleisliArrow

現時点でのユースケースは、これらの型クラスArrowの型クラスインスタンスを用いて引数1の関数や、モナドを合成することに使用されます。

引数1の関数の合成は、Scala本体でもcomposeメソッドやandThenメソッドが用意されているので、それほどニーズがあるわけではありませんが、「関数型とデータフロー(2)」で取り上げた複雑な構成のパイプラインを構築するときには有効です。

モナドの結合はflatMapメソッドなどを使えばよいのですが、モナドを合成してより大きなモナドを作るということになるとKleisli圏が登場してきます。Kleisli圏ではモナドは射として扱われるので、射の合成としてモナドを合成することができます。

kleisli圏でのモナドの合成は並列処理を行うPromiseモナドで有力な利用方法です。flatMapなどによるモナドの結合ではflatMapのポイントで並列処理がブロックされてしまうので、結合したモナド全体で並列実行したい場合には、モナドの合成を行う必要があるためです。このケースが、型クラスArrowとその関連型クラスであるCategoryの最も有効な応用になると思います。

以上のように、現時点では型クラスCategoryとArrowはほぼPromiseモナドの専用品ですが、Lens(scalaz.Lens、Lenses: A Functional Imperative)といった応用が増えてくれば、より活用の範囲が広がるのではないかと思います。

諸元

• Scala 2.9.2
• Scalaz 6.0.4